Как сложить или вычесть два вектора
Сложение векторов по правилу треугольника
Чтобы сложить два вектора $$\overline{a}$$ и $$\overline{b}$$ по правилу треугольника, необходимо:
1. Параллельно перенести векторы $$\overline{a}$$ и $$\overline{b}$$, так чтобы начало одного из векторов совпадало с концом другого.
2. Из начала вектора $$\overline{a}$$ в конец вектора $$\overline{b}$$ провести вектор $$\overline{c}$$.
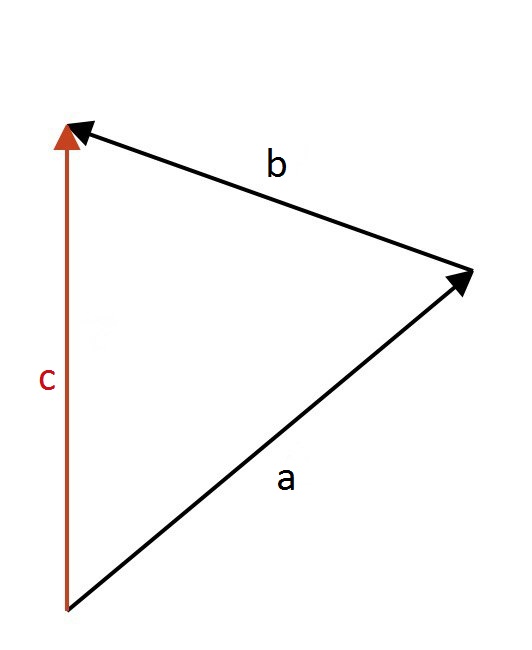Вектор $$\overline{c}$$ – есть сумма векторов $$\overline{a}$$ и $$\overline{b}$$
$$\overline{a} + \overline{b} = \overline{c}$$
Вычитание векторов по правилу треугольника
Чтобы вычесть два вектора $$\overline{a}$$ и $$\overline{b}$$ по правилу треугольника, необходимо:
1. Параллельно перенести векторы $$\overline{a}$$ и $$\overline{b}$$, так чтобы начало одного из векторов совпадало с началом другого.
2. Из конца вектора $$\overline{b}$$ в конец вектора $$\overline{a}$$ провести вектор $$\overline{c}$$.
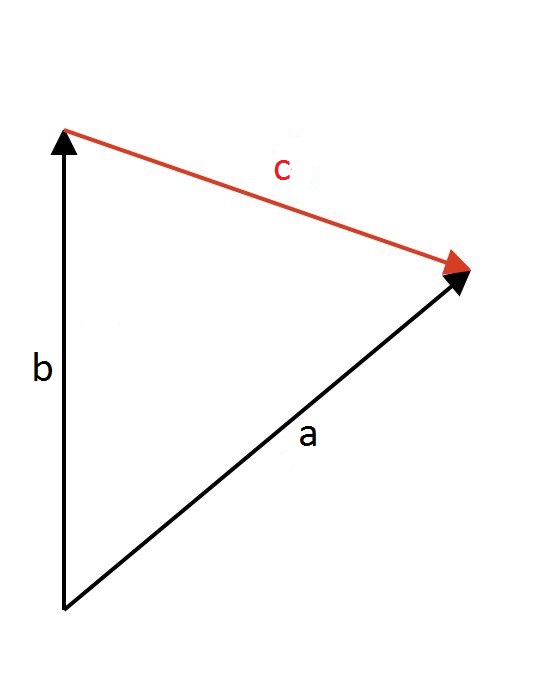Вектор $$\overline{c}$$ – есть разность векторов $$\overline{a}$$ и $$\overline{b}$$
$$\overline{a} - \overline{b} = \overline{c}$$
Как сложить два вектора, координаты которых заданы точками
Найдем сумму векторов плоскости. Координаты обоих векторов заданны точками:
Координаты точки $$A$$ вектора $$\overline{AB}$$: $$A(5\,;\,9)$$
Координаты точки $$B$$ вектора $$\overline{AB}$$: $$B(-2\,;\,11)$$
Координаты точки $$C$$ вектора $$\overline{CD}$$: $$C(0\,;\,12)$$
Координаты точки $$D$$ вектора $$\overline{CD}$$: $$B(-3\,;\,1)$$
Вычислим координаты первого вектора по двум точкам $$A$$ и $$B$$
$$\overline{AB} = \{B_x - A_x \,;\, B_y - A_y\}$$
$$\overline{AB} = \left\{-2 - 5\, ; \,11 - 9\right\} = $$$$\left\{-7\, ; \,2\right\}$$
Вычислим координаты второго вектора по двум точкам $$C$$ и $$D$$
$$\overline{CD} = \{D_x - C_x \,;\, D_y - C_y\}$$
$$\overline{CD} = \left\{-3 - 0\, ; \,1 - 12\right\} = $$$$\left\{-3\, ; \,-11\right\}$$
Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов $$\overline{AB}$$ и $$\overline{CD}$$ будет вектор $$\overline{c}$$.
Координаты вектора $$\overline{AB}$$
$$\overline{AB}$$$$\left\{-7\, ; \,2\right\}$$
Координаты вектора $$\overline{CD}$$
$$\overline{CD}$$$$\left\{-3\, ; \,-11\right\}$$
$$\overline{c} = \overline{AB}+\overline{CD} = \left\{AB_x + CD_x \, ; \, AB_y + CD_y\right\}$$
$$\overline{c} = \left\{-7+\left(-3\right)\, ; \,2+\left(-11\right)\right\} = $$$$\left\{-10\, ; \,-9\right\}$$
$$\overline{AB}+\overline{CD} = $$$$\left\{-10\, ; \,-9\right\}$$
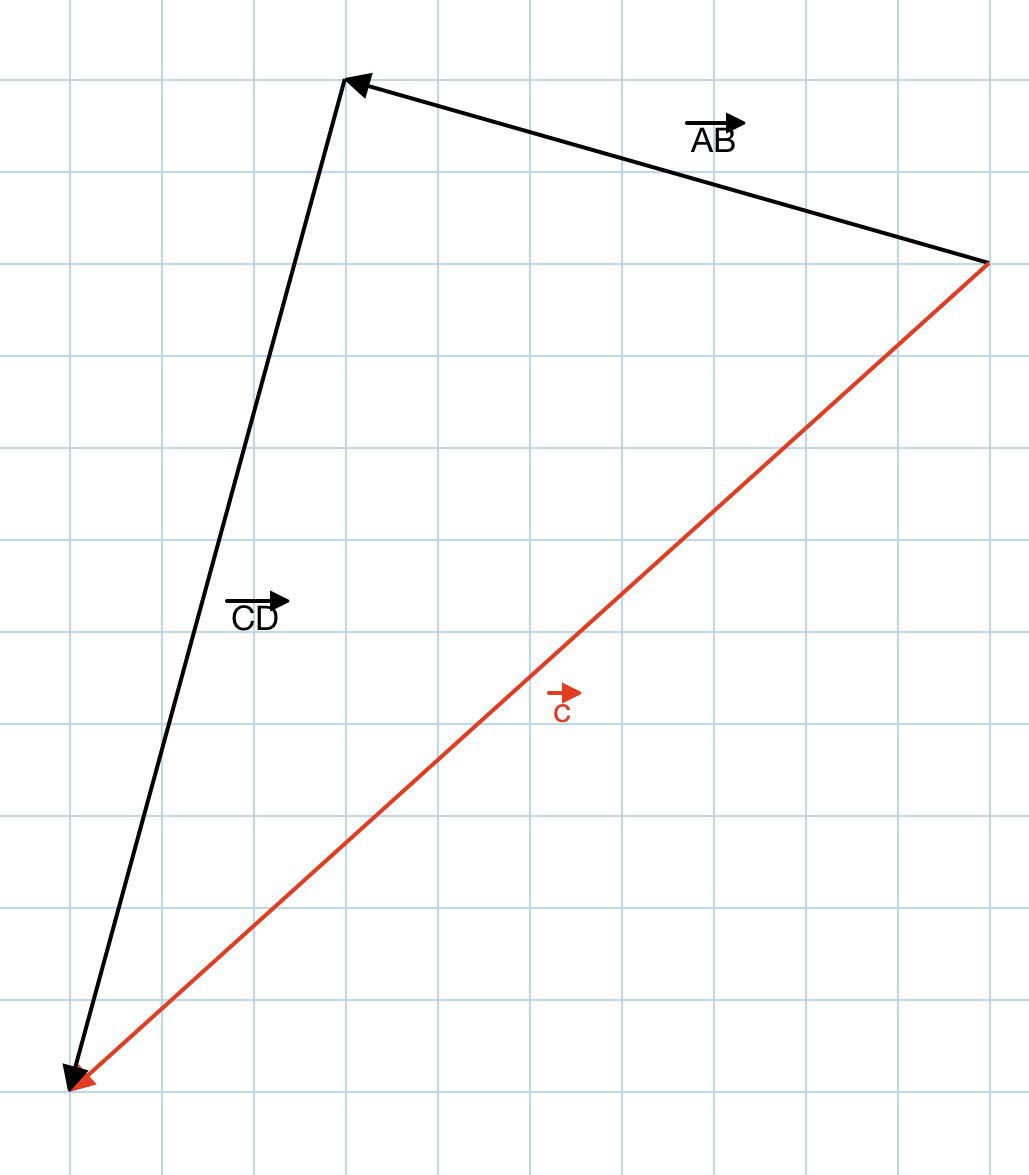$$\overline{c} = \overline{AB} + \overline{CD}$$
Как вычесть два вектора, координаты которых заданы точками
Пример. Найдем разность векторов пространства. Координаты обоих векторов заданны точками.
Координаты точки $$A$$ вектора $$\overline{AB}$$: $$A(1\,;\,-3\,;\,9)$$
Координаты точки $$B$$ вектора $$\overline{AB}$$: $$B(5\,;\,0\,;\,2)$$
Координаты точки $$C$$ вектора $$\overline{CD}$$: $$C(10\,;\,7\,;\,4)$$
Координаты точки $$D$$ вектора $$\overline{CD}$$: $$B(-8\,;\,11\,;\,6)$$
Вычислим координаты первого вектора по двум точкам $$A$$ и $$B$$
$$\overline{AB} = \{B_x - A_x \,;\, B_y - A_y \,;\, B_z - A_z\}$$
$$\overline{AB} = \left\{5 - 1\, ; \,0 - \left(-3\right)\, ; \,2 - 9\right\} = $$$$\left\{4\, ; \,3\, ; \,-7\right\}$$
Вычислим координаты второго вектора по двум точкам $$C$$ и $$D$$
$$\overline{CD} = \{D_x - C_x \,;\, D_y - C_y \,;\, D_z - C_z\}$$
$$\overline{CD} = \left\{-8 - 10\, ; \,11 - 7\, ; \,6 - 4\right\} = $$$$\left\{-18\, ; \,4\, ; \,2\right\}$$
Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов $$\overline{AB}$$ и $$\overline{CD}$$ будет вектор $$\overline{c}$$.
Координаты вектора $$\overline{AB}$$
$$\overline{AB}$$$$\left\{4\, ; \,3\, ; \,-7\right\}$$
Координаты вектора $$\overline{CD}$$
$$\overline{CD}$$$$\left\{-18\, ; \,4\, ; \,2\right\}$$
$$\overline{c} = \overline{AB}-\overline{CD} = \left\{AB_x - CD_x \, ; \, AB_y - CD_y\, ; \, AB_z - CD_z\right\}$$
$$\overline{c} = \left\{4-\left(-18\right)\, ; \,3-4\, ; \,-7-2\right\} = $$$$\left\{22\, ; \,-1\, ; \,-9\right\}$$
$$\overline{AB}-\overline{CD} = $$$$\left\{22\, ; \,-1\, ; \,-9\right\}$$
Вычитание векторов в координатном представлении
Найдем разность векторов плоскости.
Координаты вектора $$\overline{a}$$
$$\overline{a}$$$$\left\{5\, ; \,9\right\}$$
Координаты вектора $$\overline{b}$$
$$\overline{b}$$$$\left\{-1\, ; \,7\right\}$$
Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов $$\overline{a}$$ и $$\overline{b}$$ будет вектор $$\overline{c}$$.
$$\overline{c} = \overline{a}-\overline{b} = \left\{a_x - b_x \, ; \, a_y - b_y\right\}$$
$$\overline{c} = \left\{5-\left(-1\right)\, ; \,9-7\right\} = $$$$\left\{6\, ; \,2\right\}$$
$$\overline{a}-\overline{b} = $$$$\left\{6\, ; \,2\right\}$$
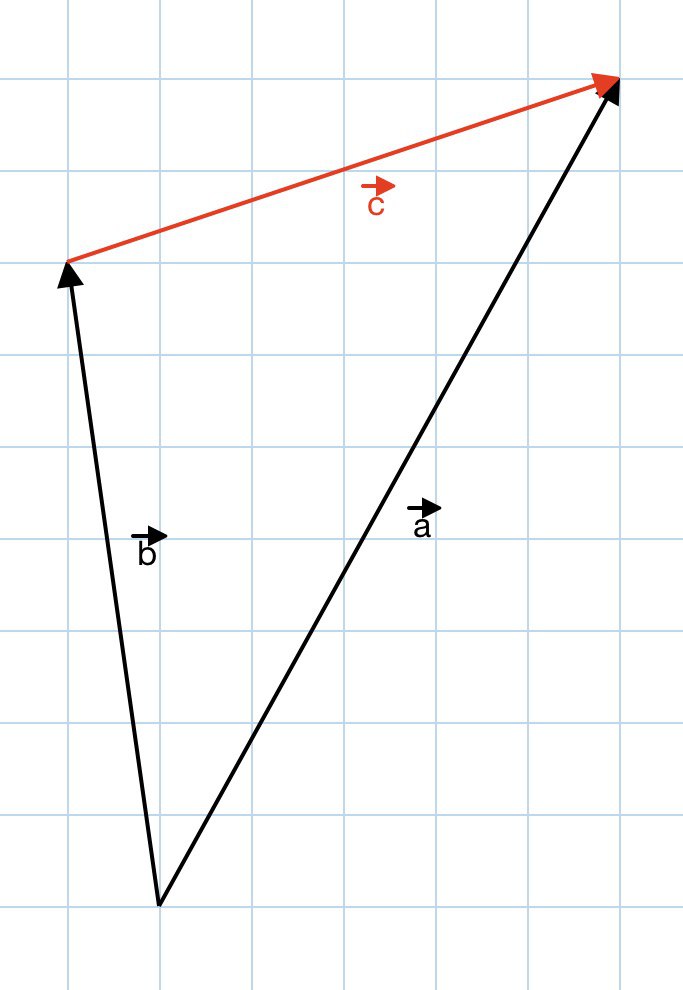$$\overline{c} = \overline{a} - \overline{b}$$
Сложение векторов в координатном представлении
Пример. Найдем сумму векторов пространства.
Координаты вектора $$\overline{a}$$
$$\overline{a}$$$$\left\{5\, ; \,1\, ; \,7\right\}$$
Координаты вектора $$\overline{b}$$
$$\overline{b}$$$$\left\{2\, ; \,4\, ; \,6\right\}$$
Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов $$\overline{a}$$ и $$\overline{b}$$ будет вектор $$\overline{c}$$.
$$\overline{c} = \overline{a}+\overline{b} = \left\{a_x + b_x \, ; \, a_y + b_y\, ; \, a_z + b_z\right\}$$
$$\overline{c} = \left\{5+2\, ; \,1+4\, ; \,7+6\right\} = $$$$\left\{7\, ; \,5\, ; \,13\right\}$$
$$\overline{a}+\overline{b} = $$$$\left\{7\, ; \,5\, ; \,13\right\}$$