Как проверить являются ли два вектора коллинеарными (параллельными)
Если два ненулевых вектора $$\overline{a}$$ и $$\overline{b}$$ лежат на одной прямой или на параллельных прямых, то такие векторы называются – коллинеарными.
Сонаправленные векторы $$\overline{a}\mathrel{\uparrow\uparrow}\overline{b}$$ – одинаково направленные коллинеарные векторы.
Антиколлинеарные векторы $$\overline{a}\mathrel{\uparrow\downarrow}\overline{b}$$ – противоположено направленные коллинеарные векторы.
Коллинеарные векторы обозначаются как: $$\overline{a}\parallel\overline{b}$$.
Определить что векторы $$\overline{a} = \{a_x\,;\,a_y;\,a_z\}$$ и $$\overline{b} = \{b_x\,;\,b_y;\,b_z\}$$ являются коллинеарными можно если вычислить их векторное произведение. Если все координаты векторного произведения векторов равны нулю, то векторы коллинеарны.
Например, найдем векторное произведение векторов $$\overline{a} = \left\{6\, ; \,10\, ; \,20\right\}$$ и $$\overline{b} = \left\{3\, ; \,5\, ; \,10\right\}$$
$$\overline{a} = \left\{6\, ; \,10\, ; \,20\right\}$$
$$\overline{b} = \left\{3\, ; \,5\, ; \,10\right\}$$
В правом ортонормированном базисе векторное произведение векторов $$\overline{a}$$ и $$\overline{b}$$ вычисляется по формуле:
$$\overline{a} \times \overline{b} = \{ a_y b_z - a_z b_y \, ; \, a_z b_x - a_x b_z \, ; \, a_x b_y - a_y b_x\}$$
$$\overline{a} \times \overline{b} = $$$$\left\{\left(10 \cdot 10 \right) - \left(20 \cdot 5 \right)\, ; \,\left(20 \cdot 3 \right) - \left(6 \cdot 10 \right)\, ; \, \left(6 \cdot 5 \right) - \left(10 \cdot 3 \right)\right\} = $$$$\left\{0\, ; \,0\, ; \,0\right\}$$
$$\overline{a} \times \overline{b} = $$$$\left\{0\, ; \,0\, ; \,0\right\}$$
Все координаты векторного произведения векторов равны нулю, следовательно, векторы $$\overline{a}$$ и $$\overline{b}$$ коллинеарны.
Векторы $$\overline{a} = \{a_x\,;\,a_y\}$$ и $$\overline{b} = \{b_x\,;\,b_y\}$$ коллинеарны если определитель, составленный из координат данных векторов, равен нулю:
$$ \begin{vmatrix}a_x&a_y\\b_x&b_y\\\end{vmatrix} = 0$$
Например, найдем векторное произведение векторов $$\overline{a} = \left\{6\, ; \,10\right\}$$ и $$\overline{b} = \left\{3\, ; \,5\right\}$$
Для матрицы размерности 2 × 2 значение определителя вычисляется по формуле:
$$det A = \begin{vmatrix}a&c\\b&d\\\end{vmatrix} = ad - bc$$
$$det A = \begin{vmatrix}6&10\\3&5\\\end{vmatrix} = \left(6 \cdot 5\right) - \left(3 \cdot 10\right) = 0$$
Определитель равен нулю, следовательно, векторы $$\overline{a}$$ и $$\overline{b}$$ коллинеарны.
Условия коллинеарности векторов
Для векторов $$\overline{a} = \{a_x\,;\,a_y\}$$ и $$\overline{b} = \{b_x\,;\,b_y\}$$ определить являются ли векторы коллинеарными можно если координаты векторов связаны отношением:
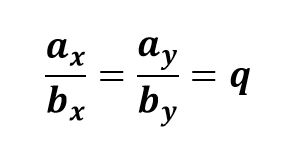Условие коллинеарности векторов
$$\overline{a} = \{a_x\,;\,a_y\}$$
$$\overline{b} = \{b_x\,;\,b_y\}$$
$$q$$ – коэффициент пропорциональности
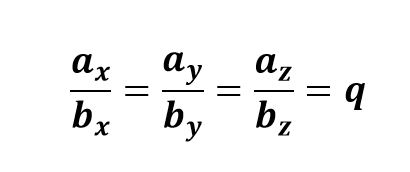Условие коллинеарности векторов
$$\overline{a} = \{a_x\,;\,a_y;\,a_z\}$$
$$\overline{b} = \{b_x\,;\,b_y;\,b_z\}$$
$$q$$ – коэффициент пропорциональности
Если коэффициент пропорциональности $$q > 0$$, то векторы $$\overline{a}$$ и $$\overline{b}$$ сонаправленны.
Если коэффициент пропорциональности $$q < 0$$, то векторы $$\overline{a}$$ и $$\overline{b}$$ антиколлинеарные, т.е. противоположно направлены.
Чтобы проверить выполняется ли равенство необходимо составить систему уравнений и вычислить коэффициент пропорциональности $$q$$ в каждом уравнении:
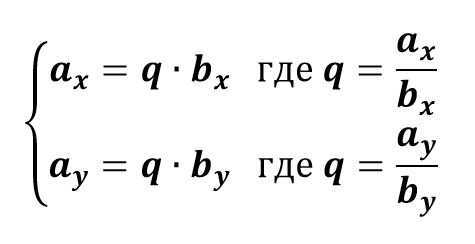$$\overline{a} = \{a_x\,;\,a_y\}$$
$$\overline{b} = \{b_x\,;\,b_y\}$$
$$q$$ – коэффициент пропорциональности
Если в первом и во втором уравнении коэффициенты пропорциональности $$q$$ равны, то координаты векторов пропорциональны и векторы коллинеарны.
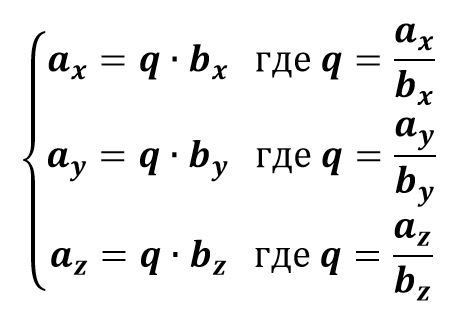$$\overline{a} = \{a_x\,;\,a_y;\,a_z\}$$
$$\overline{b} = \{b_x\,;\,b_y;\,b_z\}$$
$$q$$ – коэффициент пропорциональности
Если в первом, втором и в третьем уравнении коэффициенты пропорциональности $$q$$ равны, то координаты векторов пропорциональны и векторы коллинеарны.
Пример 1. Определим, являются ли два вектора плоскости $$\overline{a}\{a_x\,;\,a_y\} = \overline{a}\left\{2\,;\,-12\right\}$$ и $$\overline{b}\{b_x\,;\,b_y\} = \overline{b}\left\{0\,;\,5\right\}$$ коллинеарными (параллельными).
Проверим, есть ли для векторов $$\overline{a}$$ и $$\overline{b}$$ коэффициент пропорциональности $$q$$ (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
$$\overline{a}\{a_x\,;\,a_y\} = \overline{a}\left\{2\,;\,-12\right\}$$
$$\overline{b}\{b_x\,;\,b_y\} = \overline{b}\left\{0\,;\,5\right\}$$
$$\begin{cases}a_x=q\cdot b_x\\[10pt]a_y=q\cdot b_y\end{cases}$$
$$\begin{cases}2=q\cdot 0\\[10pt]-12=q\cdot 5\rightarrow q=-\frac{12}{5}\end{cases}$$
Сделаем проверку, подставим значение коэффициента $$q$$ в уравнения системы:
$$\overline{a}$$$$ \,\nparallel\, $$$$\overline{b}$$ $$\Leftrightarrow\begin{cases}2\neq-\frac{12}{5}\cdot 0\\[10pt]-12=-\frac{12}{5}\cdot 5\end{cases}$$
Коэффициент пропорциональности $$q$$ не имеет одинаковое значение во всех уравнениях системы. Следовательно, система несовместима и не имеет решений. Координаты векторов $$\overline{a}$$ и $$\overline{b}$$ не пропорциональны, значит векторы $$\overline{a}$$ и $$\overline{b}$$ не коллинеарны.
Пример 2. Определим, являются ли два вектора пространства $$\overline{a}\{a_x\,;\,a_y\,;\,a_z\} = \overline{a}\left\{-3\,;\,2\,;\,0\right\}$$ и $$\overline{b}\{b_x\,;\,b_y\,;\,b_z\} = \overline{b}\left\{-1\,;\,-7\,;\,9\right\}$$ коллинеарными (параллельными).
Проверим, есть ли для векторов $$\overline{a}$$ и $$\overline{b}$$ коэффициент пропорциональности $$q$$ (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
$$\overline{a}\{a_x\,;\,a_y\,;\,a_z\} = \overline{a}\left\{-3\,;\,2\,;\,0\right\}$$
$$\overline{b}\{b_x\,;\,b_y\,;\,b_z\} = \overline{b}\left\{-1\,;\,-7\,;\,9\right\}$$
$$\begin{cases}a_x=q\cdot b_x\\[10pt]a_y=q\cdot b_y\\[10pt]a_z=q\cdot b_z\end{cases}$$
$$\begin{cases}q = \dfrac{a_x}{b_x}= \dfrac{-3}{-1}\\[10pt]q = \dfrac{a_y}{b_y}=\dfrac{2}{-7}\\[10pt]q = \dfrac{a_z}{b_z}=\dfrac{0}{9}\end{cases}$$
$$\overline{a}$$$$ \,\nparallel\, $$$$\overline{b}$$ $$\Leftrightarrow\begin{cases}q = 3\\[10pt]q = -\frac{2}{7}\\[10pt]q = 0\end{cases}$$
Коэффициент пропорциональности $$q$$ не имеет одинаковое значение во всех уравнениях системы. Следовательно, система несовместима и не имеет решений. Координаты векторов $$\overline{a}$$ и $$\overline{b}$$ не пропорциональны, значит векторы $$\overline{a}$$ и $$\overline{b}$$ не коллинеарны.