Как вычислить скалярное произведение векторов через координаты
Скалярным произведением двух векторов $$\overline{a}$$ и $$\overline{b}$$ – называется сумма произведений координат данных векторов:
Если
$$\overline{a} = \{a_x\,;\,a_y\}$$ и $$\overline{b} = \{b_x\,;\,b_y\}$$, тогда:
$$ \overline{a} \cdot \overline{b} = a_{x} b_{x} + a_{y} b_{y}$$
Если
$$\overline{a} = \{a_x\,;\,a_y\,;\,a_z\}$$ и $$\overline{b} = \{b_x\,;\,b_y\,;\,b_z\}$$, тогда:
$$ \overline{a} \cdot \overline{b} = a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}$$
Если координаты векторов $$\overline{a}$$ и $$\overline{b}$$ заданы точками, а именно:
Вектор $$\overline{a}$$ задан точками $$A$$ и $$B$$, где
$$A = (A_x\,;\,A_y)$$
$$B = (B_x\,;\,B_y)$$
Вектор $$\overline{b}$$ задан точками $$C$$ и $$D$$, где
$$C = (C_x\,;\,C_y)$$
$$D = (D_x\,;\,D_y)$$
то скалярное произведение определяется как:
$$ \overline{a} \cdot \overline{b} = (B_x - A_x)(D_x - C_x) + (B_y - A_y)(D_y - C_y)$$
Если координаты векторов $$\overline{a}$$ и $$\overline{b}$$ заданы точками, а именно:
Вектор $$\overline{a}$$ задан точками $$A$$ и $$B$$, где
$$A = (A_x\,;\,A_y\,;\,A_z)$$
$$B = (B_x\,;\,B_y\,;\,B_z)$$
Вектор $$\overline{b}$$ задан точками $$C$$ и $$D$$, где
$$C = (C_x\,;\,C_y\,;\,C_z)$$
$$D = (D_x\,;\,D_y\,;\,D_z)$$
то скалярное произведение определяется как:
$$ \overline{a} \cdot \overline{b} = (B_x - A_x)(D_x - C_x) + (B_y - A_y)(D_y - C_y) + (B_z - A_z)(D_z - C_z)$$
Примеры вычисления скалярного произведения векторов по координатам
Пример 1. Найдем скалярное произведение векторов плоскости.
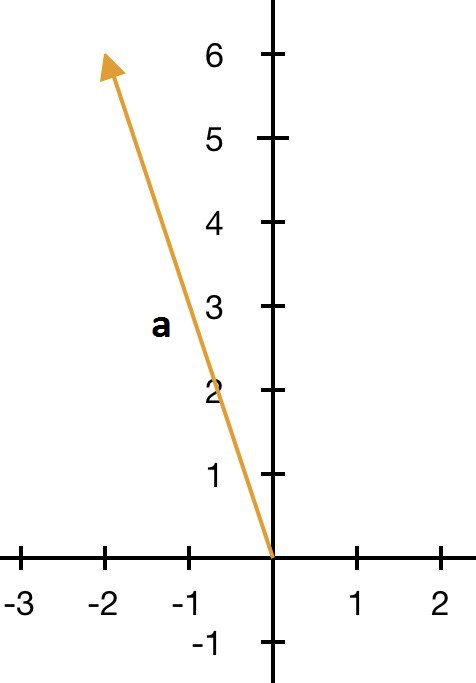Координаты вектора $$\overline{a} = \left\{-2\, ; \,6\right\}$$
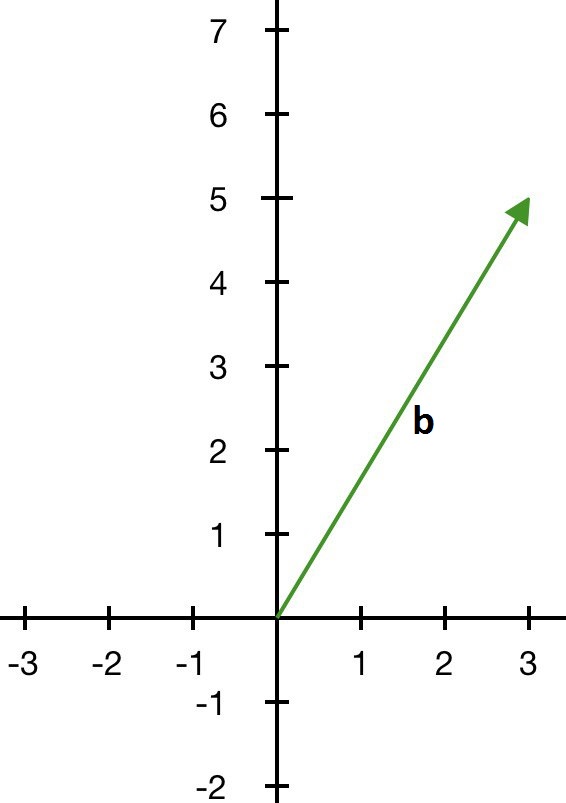Координаты вектора $$\overline{b} = \left\{3\, ; \,5\right\}$$
$$\overline{a} \cdot \overline{b} = a_{x} b_{x} + a_{y} b_{y}$$
$$\overline{a} \cdot \overline{b} = \left( -2 \cdot 3\right) + \left(6 \cdot 5\right) = $$$$24$$
Пример 2. Найдем скалярное произведение векторов пространства.
Координаты вектора $$\overline{a} = \left\{5\, ; \,1\, ; \,7\right\}$$
Координаты вектора $$\overline{a} = \left\{2\, ; \,4\, ; \,6\right\}$$
$$\overline{a} \cdot \overline{b} = a_{x} b_{x} + a_{y} b_{y}+ a_{z} b_{z}$$
$$\overline{a} \cdot \overline{b} = \left( 5 \cdot 2\right) + \left(1 \cdot 4\right)+ \left(7 \cdot 6\right) = $$$$56$$
Пример 3. Найдем скалярное произведение векторов плоскости, координаты которых заданы точками.
Вектор $$\overline{a}$$ задан точками $$A$$ и $$B$$, где
$$A = (5\,;\,9)$$
$$B = (-2\,;\,11)$$
Вектор $$\overline{b}$$ задан точками $$C$$ и $$D$$, где
$$C = (0\,;\,12)$$
$$D = (-3\,;\,1)$$
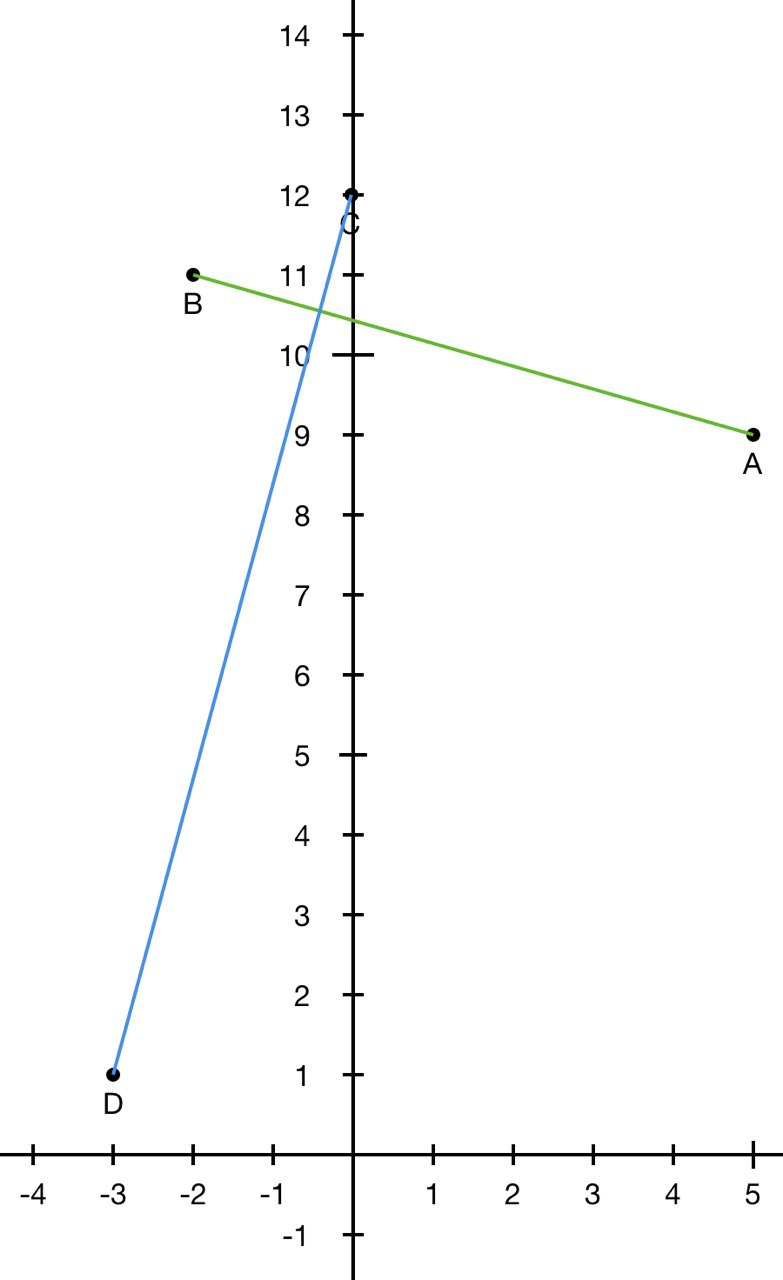Точки $$A$$, $$B$$, $$C$$, $$D$$
Воспользуемся формулой: $$ \overline{a} \cdot \overline{b} = (B_x - A_x)(D_x - C_x) + (B_y - A_y)(D_y - C_y)$$ тогда,
$$ \overline{a} \cdot \overline{b} = (-2 - 5)\cdot(-3 - 0) + (11 - 9)\cdot(1 - 12) = -1$$
Этот пример можно решить по-другому, вычислив сначала координаты векторов по точкам, а затем зная координаты вычислить скалярное произведение:
Вычислим координаты первого вектора по двум точкам $$A$$ и $$B$$
$$\overline{AB} = \{B_x - A_x \,;\, B_y - A_y\}$$
$$\overline{AB} = \left\{-2 - 5\, ; \,11 - 9\right\} = \left\{-7\, ; \,2\right\}$$
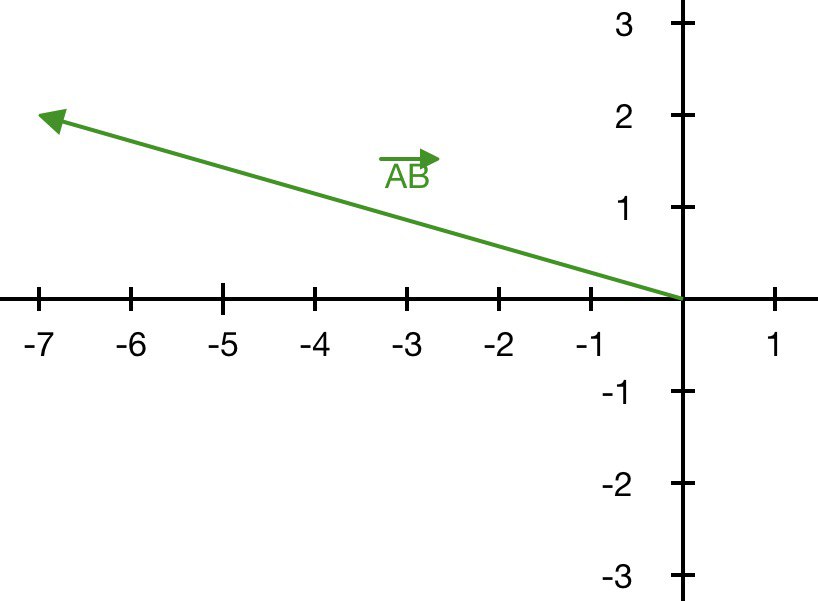Вектор $$\overline{AB}$$
Вычислим координаты второго вектора по двум точкам $$C$$ и $$D$$
$$\overline{CD} = \{D_x - C_x \,;\, D_y - C_y\}$$
$$\overline{CD} = \left\{-3 - 0\, ; \,1 - 12\right\} = $$$$\left\{-3\, ; \,-11\right\}$$
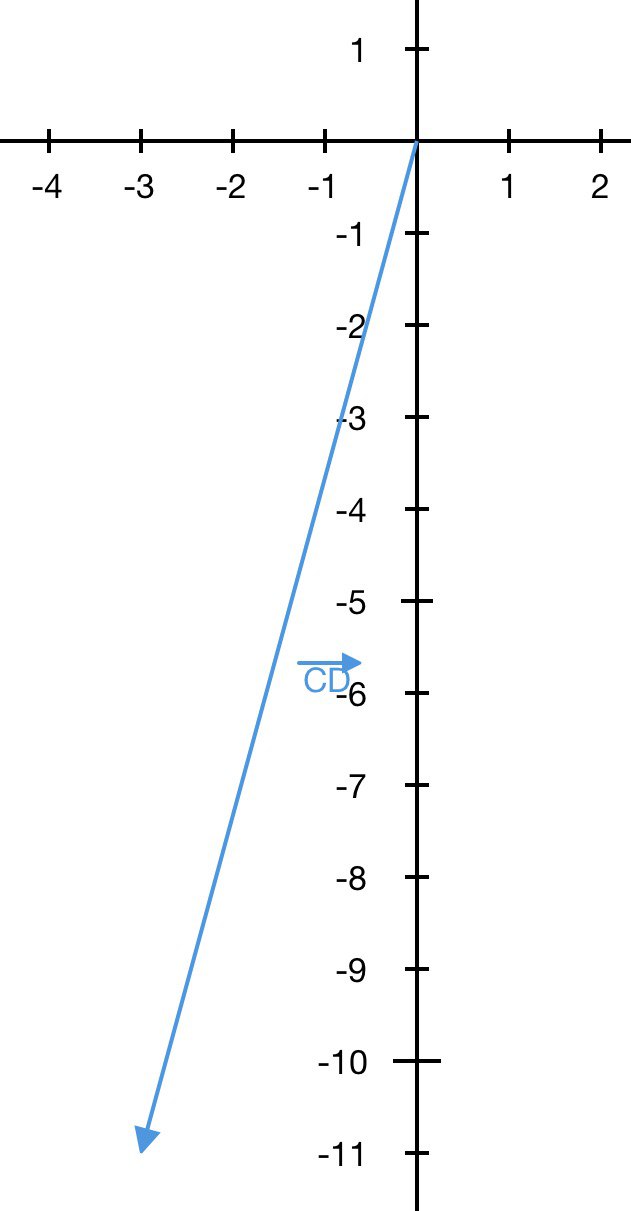Вектор $$\overline{CD}$$
Найдем скалярное произведение векторов: $$\overline{AB}$$ и $$\overline{CD}$$
$$\overline{AB} \cdot \overline{CD} = AB_{x} CD_{x} + AB_{y} CD_{y}$$
$$\overline{AB} \cdot \overline{CD} = \left( -7 \cdot \left(-3\right)\right) + \left(2 \cdot \left(-11\right)\right) = $$$$-1$$
Пример 4. Найдем скалярное произведение векторов пространства. Координаты обоих векторов заданны точками.
Вектор $$\overline{a}$$ задан точками $$A$$ и $$B$$, где
$$A = (-1\,;\,3,;\,7)$$
$$B = (4\,;\,8\,;\,-3)$$
Вектор $$\overline{b}$$ задан точками $$C$$ и $$D$$, где
$$C = (-5\,;\,2\,;\,1)$$
$$D = (13\,;\,1\,;\,4)$$
Воспользуемся формулой:
$$ \overline{a} \cdot \overline{b} = (B_x - A_x)(D_x - C_x) + (B_y - A_y)(D_y - C_y) + (B_z - A_z)(D_z - C_z)$$
$$ \overline{a} \cdot \overline{b} = (4 - (-1))\cdot(13 - (-5)) + (8 - 3)\cdot(1 - 2) + (-3 - 7)\cdot(4 - 1) = 55$$
Как в предыдущем примере решим пример иначе, сначала вычислив координаты векторов по точкам:
Вычислим координаты первого вектора по двум точкам $$A$$ и $$B$$
$$\overline{AB} = \{B_x - A_x \,;\, B_y - A_y \,;\, B_z - A_z\}$$
$$\overline{AB} = \left\{4 - \left(-1\right)\, ; \,8 - 3\, ; \,-3 - 7\right\} = $$$$\left\{5\, ; \,5\, ; \,-10\right\}$$
Вычислим координаты второго вектора по двум точкам $$C$$ и $$D$$
$$\overline{CD} = \{D_x - C_x \,;\, D_y - C_y \,;\, D_z - C_z\}$$
$$\overline{CD} = \left\{13 - \left(-5\right)\, ; \,1 - 2\, ; \,4 - 1\right\} = $$$$\left\{18\, ; \,-1\, ; \,3\right\}$$
$$\overline{AB} \cdot \overline{CD} = AB_{x} CD_{x} + AB_{y} CD_{y}+ AB_{z} CD_{z}$$
$$\overline{AB} \cdot \overline{CD} = \left( 5 \cdot 18\right) + \left(5 \cdot \left(-1\right)\right)+ \left(-10 \cdot 3\right) = $$ $$55$$