Как найти модуль вектора
Модулем вектора $$|\overline{AB}|$$ называется число, равное расстоянию между начальной и конечной точками вектора.
Для того чтобы найти модуль (длину) вектора, если известны координаты его начальной и конечной точек необходимо воспользоваться одной из формул:
$$|\overline{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2}}$$ - для вычисления длины вектора плоскости
$$|\overline{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2} + {(B_z - A_z)}^{2}}$$ - для вычисления длины вектора пространства
Для того чтобы найти модуль (длину) вектора, если известны его координаты необходимо воспользоваться одной из формул:
$$|\overline{a}| = \sqrt{{a_x}^{2} + {a_y}^{2}}$$ - для вычисления длины вектора плоскости
$$|\overline{a}| = \sqrt{{a_x}^{2} + {a_y}^{2} + {a_z}^{2}}$$ - для вычисления длины вектора пространства
Пример 1. Найдем длину вектора плоскости с координатами начальной и конечной точек $$A(x\,;\,y)$$ и точки $$B(x\,;\,y)$$, где $$A(1\,;\,9)$$ и $$A(4\,;\,7)$$.
Тогда согласно формуле:
$$ B_x = 4$$
$$ A_x = 1$$
$$ B_y = 7$$
$$ A_y = 9$$
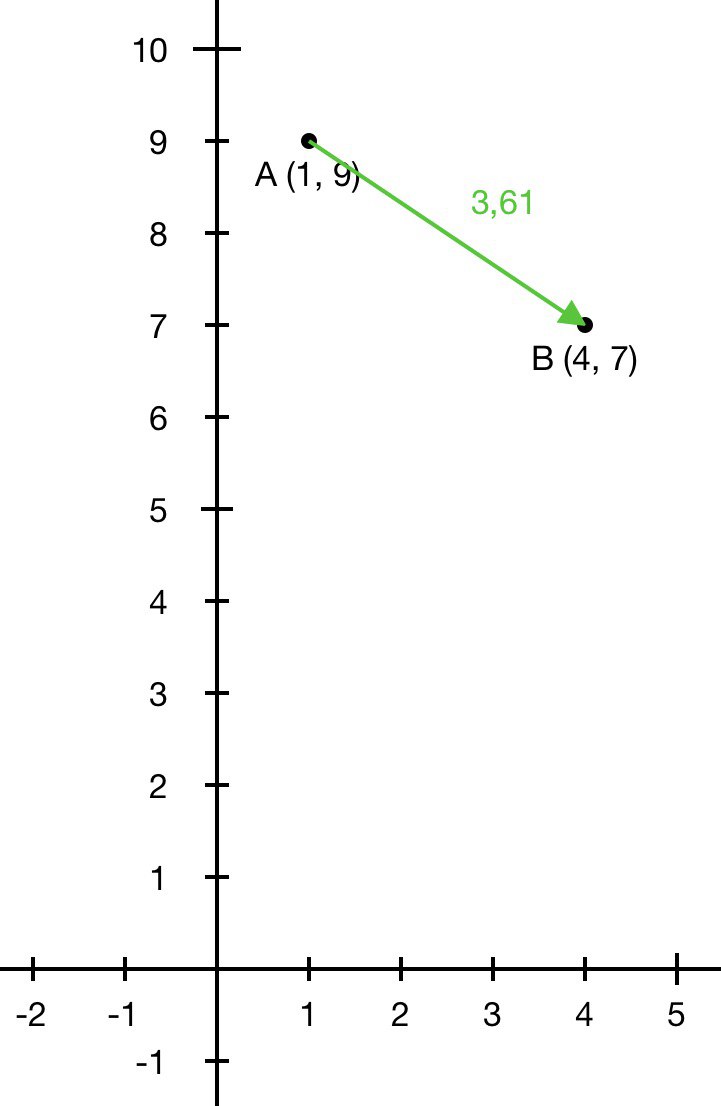Вектор $$|\overline{AB}|$$
Подставим значения в формулу и найдем модуль вектора $$|\overline{AB}|$$
$$|\overline{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2}} $$
$$|\overline{AB}| = \sqrt{{\left(4 - 1\right)}^{2} + {\left(7 - 9\right)}^{2}}=$$$$\sqrt{{\left(3\right)}^{2} + {\left(-2\right)}^{2}}=$$$$\sqrt{9+4}=$$$$\sqrt{13}=3.60555127546399$$
$$|\overline{AB}| =\sqrt{13}=3.60555127546399$$
Пример 2. Найдем длину вектора пространства с координатами начальной и конечной точек $$A(x\,;\,y\,;\,z)$$ и точки $$B(x\,;\,y\,;\,z)$$, где $$A(1\,;\,-9\,;\,6)$$ и $$B(4\,;\,-2\,;\,7)$$.
Тогда согласно формуле
$$ A_x = 1$$
$$A_y = -9$$
$$A_z = 6$$
$$B_x = 4$$
$$B_y = -2$$
$$B_z = 7$$
Подставим значения в формулу и найдем длину вектора $$|\overline{AB}|$$
$$|\overline{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2} + {(B_z - A_z)}^{2}} $$
$$|\overline{AB}| = \sqrt{{\left(4 - 1\right)}^{2} + {\left(-2 - \left(-9\right)\right)}^{2} + {\left(7 - 6\right)}^{2}}=$$$$\sqrt{{\left(3\right)}^{2} + {\left(7\right)}^{2} + {\left(1\right)}^{2}}=$$$$\sqrt{9+49+1}=$$$$\sqrt{59}=7.68114574786861$$
$$|\overline{AB}| =\sqrt{59}=7.68114574786861$$
Пример 3. Найдем длину вектора $$\overline{a}$$ плоскости с координатами $$\overline{a}\{x\,;\,y\}$$, где $$\overline{a}\{3\,;\,8\}$$.
Тогда согласно формуле:
$$a_x = 3$$
$$a_y = 8$$
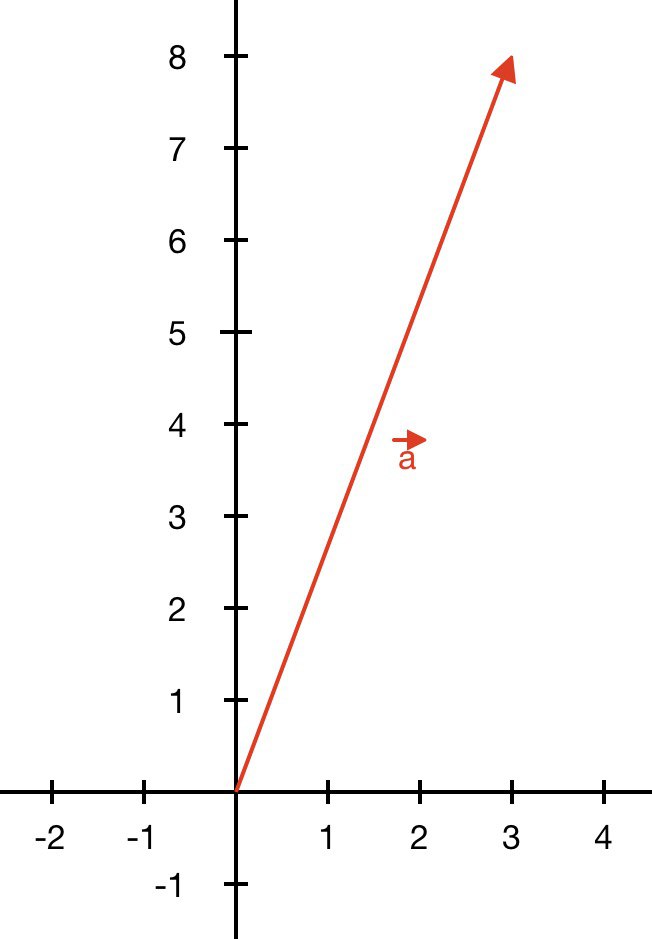Вектор $$|\overline{a}|$$
Подставим значения в формулу и найдем модуль вектора $$|\overline{a}|$$
$$|\overline{a}| = \sqrt{{a_x}^{2} + {a_y}^{2}}$$
$$|\overline{a}| = \sqrt{{3}^{2} + {8}^{2}}=$$$$\sqrt{9+64}=$$$$\sqrt{73}=8.54400374531753$$
$$|\overline{a}| =$$$$\sqrt{73}=8.54400374531753$$
Пример 4. Найдем длину вектора $$\overline{a}$$ пространства с координатами $$\overline{a}\{x\,;\,y\,;\,z\}$$, где $$\overline{a}\{4\,;\,2\,;\,7\}$$.
Тогда согласно формуле:
$$a_x = 4$$
$$a_y = 2$$
$$a_z = 7$$
Подставим значения в формулу и найдем модуль вектора $$|\overline{a}|$$
$$|\overline{a}| = \sqrt{{a_x}^{2} + {a_y}^{2} + {a_z}^{2}}$$
$$|\overline{a}| = \sqrt{{4}^{2} + {2}^{2} + {7}^{2}}=$$$$\sqrt{16+4+49}=$$$$\sqrt{69}=8.30662386291807$$
$$|\overline{a}| =$$$$\sqrt{69}=8.30662386291807$$