Как найти расстояние между точками плоскости и пространства
Расстояние между двумя точками в Евклидовом пространстве вычисляется по теореме Пифагора $$c^2=a^2+b^2$$ и выражается формулой:
$$|\textbf{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2}}$$ - для вычисления длины отрезка плоскости
$$|\textbf{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2} + {(B_z - A_z)}^{2}}$$ - для вычисления длины отрезка пространства
Расстояние между точками в Евклидовом пространстве – называется Евклидовой метрикой, либо Евклидовым расстоянием.
Пример 1. Найдем расстояния между точками плоскости с координатами $$A(x\,;\,y)$$ и точки $$B(x\,;\,y)$$, где $$A(1\,;\,9)$$ и $$B(4\,;\,7)$$.
Тогда согласно формуле:
$$B_x = 4$$
$$A_x = 1$$
$$B_y = 7$$
$$A_y = 9$$
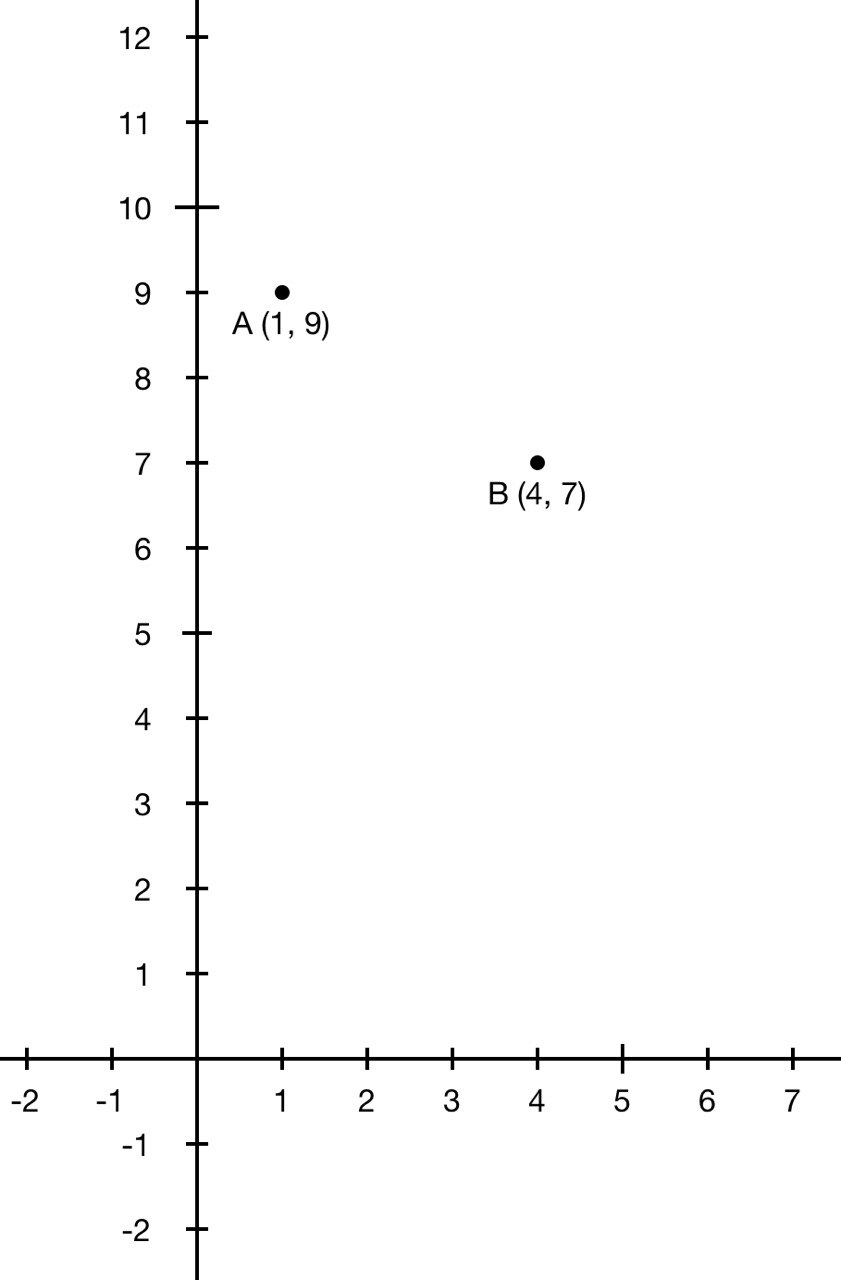Точки A и B
Подставим значения в формулу и вычислим расстояние между точками A и B:
$$|\textbf{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2}}$$
$$|\textbf{AB}| = \sqrt{{\left(4 - 1\right)}^{2} + {\left(7 - 9\right)}^{2}}=$$ $$\sqrt{{\left(3\right)}^{2} + {\left(-2\right)}^{2}}=$$ $$\sqrt{9+4}=$$ $$\sqrt{13}=3.60555127546399$$
$$|\textbf{AB}| =\sqrt{13}=3.60555127546399$$
Пример 2. Найдем расстояния между точками пространства с координатами $$A(x\,;\,y\,;\,z)$$ и точки $$B(x\,;\,y\,;\,z)$$, где $$A(5\,;\,2\,;\,9)$$ и $$A(3\,;\,6\,;\,7)$$.
Тогда согласно формуле
$$B_x = 3$$
$$A_x = 5$$
$$B_y = 6$$
$$A_y = 2$$
$$B_z = 7$$
$$A_z = 9$$
Подставим значения в формулу и вычислим расстояние между точками A и B
$$|\textbf{AB}| = \sqrt{{(B_x - A_x)}^{2} + {(B_y - A_y)}^{2} + {(B_z - A_z)}^{2}} $$
$$|\textbf{AB}| = \sqrt{{\left(3 - 5\right)}^{2} + {\left(6 - 2\right)}^{2} + {\left(7 - 9\right)}^{2}}=$$$$\sqrt{{\left(-2\right)}^{2} + {\left(4\right)}^{2} + {\left(-2\right)}^{2}}=$$$$\sqrt{4+16+4}=$$$$\sqrt{24}=4.89897948556636$$
$$|\textbf{AB}| =\sqrt{24}=4.89897948556636$$