Десятичные дроби	Ввод
$$3,9$$	3.9
$$6,012$$	6.012
$$0,209$$	0.209
Обыкновенные дроби
$$\dfrac{2}{3}$$	2/3
$$\dfrac{15}{7}$$	15/7
$$\dfrac{1}{9}$$	1/9
Возведение в степень
$${3}^{2}$$	3^2
$${{2}^{3}}^{4}$$	(2^3)^4
$$\left({\dfrac{2}{3}}\right)^{8}$$	(2/3)^8
Квадратный корень
$$\sqrt{2}$$	sqrt(2)
$$\sqrt{\dfrac{9}{15}}$$	sqrt(9/15)
$$\left(\sqrt{\dfrac{6}{7}}\right)^{3}$$	(sqrt(6/7))^3
$$2\sqrt{5}$$	2*sqrt(5)
$$\dfrac{1}{2}\sqrt{3}$$	(1/2)*sqrt(3)
Число π
$$\pi$$	pi
$$2\pi$$	2pi
$$\dfrac{3\pi}{2}$$	3pi/2
Число Эйлера e
$$e$$	Для записи числа Эйлера введите e
$${e}^{\left(\dfrac{1}{3}\right)}$$	e^(1/3)
Натуральный логарифм ln
$$\ln{3}$$	ln(3)
$$\ln{\dfrac{1}{2}}$$	ln(1/2)
$$\sqrt{\ln{5}}$$	sqrt(ln(5))
Экспоненциальная запись чисел
$$2.3e+15$$	2.3e+15
$$2.45e-35$$	2.45e-35
Абсолютная величина (модуль)
$$\lvert -5 \rvert$$	abs(-5)
$$\lvert \sqrt{2}-7 \rvert$$	abs(sqrt(2)-7)
Тригонометрические функции
Внимание! Параметр x должен быть указан в радианах. Если вам необходимо выполнить вычисления в градусах, то необходимо внутри функции сделать перевод из градусов в радианы, например, sin(45°), тогда sin(45*pi/180).
Синус sin(x)	sin(x)
Косинус cos(x)	cos(x)
Тангенс tg(x), tan(x)	tan(x)
Котангенс ctg(x), cot(x)	cot(x)
Секанс sec(x)	sec(x)
Косеканс csc(x), cosec(x)	csc(x)
Гиперболические функции
Внимание! Параметр x должен быть указан в радианах. Если вам необходимо выполнить вычисления в градусах, то необходимо внутри функции сделать перевод из градусов в радианы, например, sinh(45°), тогда sinh(45*pi/180).
Гиперболический синус sh(x), sinh(x)	sinh(x)
Гиперболический косинус ch(x), cosh(x)	cosh(x)
Гиперболический тангенс th(x), tanh(x)	tanh(x)
Гиперболический котангенс cth(x), coth(x)	coth(x)
Гиперболический секанс sch(x), sech(x)	sech(x)
Гиперболический косеканс csch(x), csch(x)	csch(x)
Обратные тригонометрические функции
Арксинус arcsin(x)	asin(x)
Арккосинус arccos(x)	acos(x)
Арктангенс arctg(x), arctan(x)	atan(x)
Арккотангенс arcctg(x), arccot(x)	acot(x)
Арксеканс arcsec(x)	asec(x)
Арккосеканс arccsc(x)	acsc(x)
Обратные гиперболические функции
Ареасинус arsh(x), arsinh(x), sin⁻¹	asinh(x)
Ареакосинус arch(x), arcosh(x), cosh⁻¹	acosh(x)
Ареатангенс arth(x), artanh(x), tanh⁻¹	atanh(x)
Ареакотангенс arcth(x), arcoth(x), coth⁻¹	acoth(x)
Ареасеканс arsch(x), arsech(x), sech⁻¹	asech(x)
Ареакосеканс arcsch(x), csch⁻¹	acsch(x)
Математические выражения
$$\dfrac{3}{\sqrt{2}} + \left({\dfrac{3}{2}}\right)^{5}$$	3/sqrt(2)+(3/2)^5
$$\dfrac{3}{\sqrt{2}\cdot\dfrac{1}{12}-\dfrac{4}{3}}$$	3/(sqrt(2)*(1/12)-3/4)
$${\left(\dfrac{5}{12} + \dfrac{3}{2} - 5\right)}^{\dfrac{1}{2}}$$	(5/12 + 3/2 - 5)^(1/2)
$$6-7\cos{\frac{3\pi}{2}}^{2}$$	6-7cos(3pi/2)^2

Скалярное произведение двух ненулевых векторов - это число, которое равно произведению длин этих векторов на косинус угла между ними.
$$\overline{a} \cdot \overline{b} = |\overline{a}| \cdot |\overline{b}| \cdot \cos{\alpha}$$

Модуль (длина) вектора $$|\overline{a}|$$

Модуль (длина) вектора $$|\overline{b}|$$

Найти модуль (длину) векторов можно при помощи калькулятора длины вектора.

Скалярное произведение двух векторов

Скалярное произведение вектора a на вектор b – есть произведение их модулей на косинус угла между ними.

|Модулем| вектора называется число, равное расстоянию между начальной и конечной точками вектора.

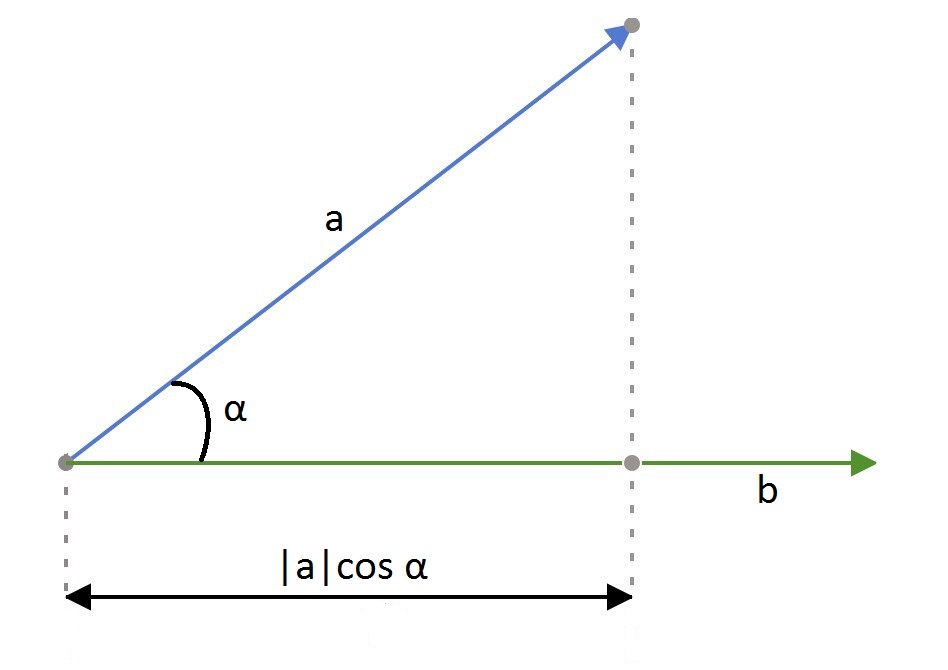$$ \overline{a} \cdot \overline{b} = |\overline{a}| \cdot |\overline{b}| \cdot \cos{\alpha}$$

Скалярное произведение обозначается как:
$$\overline{a} \cdot \overline{b}$$ или $$\textbf{a} \cdot \textbf{b}$$ либо $$\textbf{ab}$$.

Скалярное произведение двух векторов $$\overline{a}$$ и $$\overline{b}$$ можно также определить, как модуль одного из векторов умноженный на алгебраическую проекцию другого вектора:

$$ \overline{a} \cdot \overline{b} = |\overline{a}| \cdot пр_{a} \, \overline{b} $$
$$ \overline{a} \cdot \overline{b} = |\overline{b}| \cdot пр_{b} \, \overline{a} $$

Знак скалярного произведения может быть определен следующим образом:

$$\overline{a} \cdot \overline{b} > 0$$
скалярное произведение больше нуля, если угол между векторами $$\overline{a}$$ и $$\overline{b}$$ острый

$$\overline{a} \cdot \overline{b} < 0$$
скалярное произведение меньше нуля, если угол между векторами $$\overline{a}$$ и $$\overline{b}$$ тупой

$$\overline{a} \cdot \overline{b} = 0$$
скалярное произведение равно нулю, если угол между векторами $$\overline{a}$$ и $$\overline{b}$$ прямой

Скалярное произведение равно нулю, если хотя бы один из векторов нулевой.

Приведем пример, найдем скалярное произведение двух векторов $$\overline{a}$$ и $$\overline{b}$$:

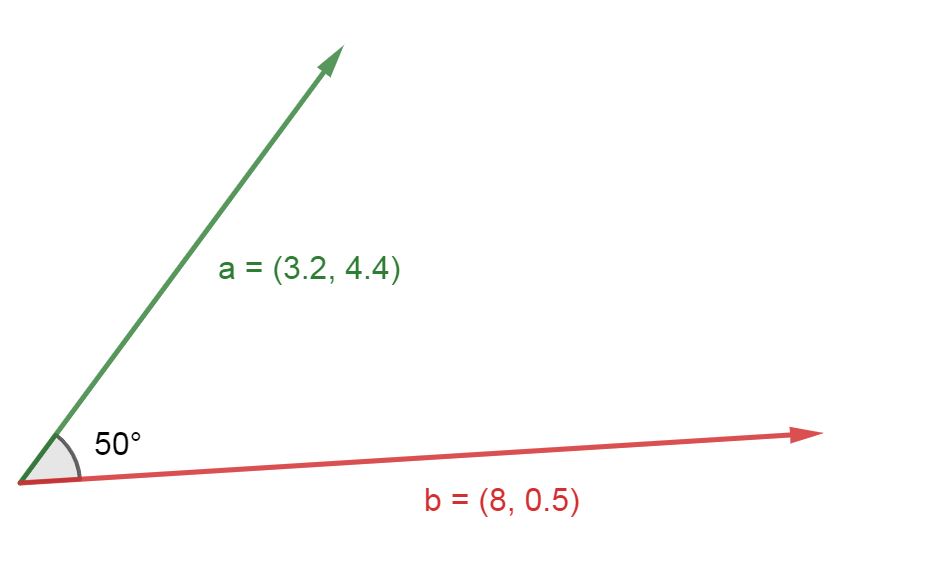**Угол между векторами $$\overline{a}$$ и $$\overline{b} = $$ 50 градусов**

Модуль (длина) вектора $$|\overline{a}| = \sqrt{{\left(3.2\right)}^{2} + {\left(4.4\right)}^{2}} = \sqrt{10.24+19.36} = 5.44058820349418$$
Модуль (длина) вектора $$|\overline{b}| = \sqrt{{8}^{2} + {\left(0.5\right)}^{2}} = \sqrt{64+0.25} = 8.0156097709407$$

Тогда, скалярное произведение двух векторов $$\overline{a}$$ и $$\overline{b}$$

$$\overline{a} \cdot \overline{b} = |\overline{a}| \cdot |\overline{b}| \cdot \cos{\alpha}$$

$$\overline{a} \cdot \overline{b} = 5.44058820349418 \cdot 8.0156097709407 \cdot \cos{50} = $$$$43.6096319635926\cdot\cos{\frac{5}{18}\pi}=28.0317310891874$$

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами