Как найти обратную матрицу с помощью матрицы алгебраических дополнений
Обратная матрица $$A$$ обозначается как $$A^{-1}$$.
Обратная матрица $$A^{-1}$$ существует только если матрица $$A$$ квадратная и ее определитель не равен нулю.
При умножении матрицы $$A$$ на обратную матрицу $$A^{-1}$$ получается единичная матрица $$E$$.
$$AA^{-1}=E$$
Обратная матрица $$A^{-1}$$ определяется как:
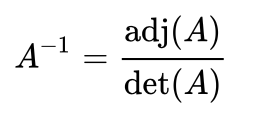
где,
$$adj A$$ - присоединенная матрица, составленная из алгебраических дополнений
$$detA$$ - определитель матрицы $$A$$
Элемент $$adj A_{ij}$$ присоединенной матрицы $$adj A$$ вычисляется по формуле:
$$adj A_{ij} = (-1)^{i+j} M_{ij}$$
где,
$$M_{ij}$$ - дополнительный минор (определитель матрицы), полученный из исходной матрицы $$A$$ путем вычеркивания i-й строки и j-го столбца.
Чтобы найти обратную матрицу $$A^{-1}$$ матрицы $$A$$ необходимо:
1. Вычислить определитель матрицы $$A$$.
2. Найти присоединённую матрицу $$adj A$$.
3. Транспонировать присоединённую матрицу $$adj A$$.
4. Разделить все элементы присоединённой матрицы $$adj A$$ на определитель $$det A$$ исходной матрицы $$A$$.
Приведем пример, найдем обратную матрицу $$A^{-1}$$ для матрицы $$A$$, размерности 2 × 2:
$$ A = \begin{bmatrix}6&2\\1&5\\\end{bmatrix}$$
Вычислим определитель матрицы $$A$$
$$det A = \sum_{j=1}^{n}(-1)^{1+j} a_{1j} M_{1j}$$
$$det A = \begin{vmatrix}6&2\\1&5\\\end{vmatrix}=28$$
Если вы хотите получить пошаговое решение нахождения определителя, то воспользуйтесь
калькулятором определителя матрицы.
Найдем присоединённую матрицу $$adj A$$ составленную из алгебраических дополнений.
Элемент $$adj A_{ij}$$ присоединенной матрицы $$adj A$$ вычисляется по формуле:
$$adj A_{ij} = (-1)^{i+j} M_{ij}$$
где $$M_{ij}$$ - дополнительный минор, полученный из исходной матрицы $$A$$ путем вычеркивания i-й строки и j-го столбца.
Исходная матрицы A состоит из 4 элементов, следовательно нам необходимо найти 4 дополнительных миноров $$M_{ij}$$:
$$M_{11}=\begin{vmatrix}\color{lightgrey}{6}&\color{lightgrey}{2}\\\color{lightgrey}{1}&5\\\end{vmatrix}=\begin{vmatrix}5\\\end{vmatrix}=5$$
$$M_{12}=\begin{vmatrix}\color{lightgrey}{6}&\color{lightgrey}{2}\\1&\color{lightgrey}{5}\\\end{vmatrix}=\begin{vmatrix}1\\\end{vmatrix}=1$$
$$M_{21}=\begin{vmatrix}\color{lightgrey}{6}&2\\\color{lightgrey}{1}&\color{lightgrey}{5}\\\end{vmatrix}=\begin{vmatrix}2\\\end{vmatrix}=2$$
$$M_{22}=\begin{vmatrix}6&\color{lightgrey}{2}\\\color{lightgrey}{1}&\color{lightgrey}{5}\\\end{vmatrix}=\begin{vmatrix}6\\\end{vmatrix}=6$$
Выпишем значения получившихся миноров:
| $$M_{11}$$ | $$=$$ | $$5$$ |
| $$M_{12}$$ | $$=$$ | $$1$$ |
| $$M_{21}$$ | $$=$$ | $$2$$ |
| $$M_{22}$$ | $$=$$ | $$6$$ |
Далее вычислим значения каждого элемента $$adj A_{ij}$$ матрицы $$adj A$$
$$adj A_{11} = (-1)^{1+1} M_{11} = 1\cdot5 = 5$$
$$adj A_{12} = (-1)^{1+2} M_{12} = -1\cdot1 = -1$$
$$adj A_{21} = (-1)^{2+1} M_{21} = -1\cdot2 = -2$$
$$adj A_{22} = (-1)^{2+2} M_{22} = 1\cdot6 = 6$$
$$adj A = \begin{bmatrix}5&-1\\-2&6\\\end{bmatrix}$$
Транспонируем присоединенную матрицу $$adj A$$
$$adj A^T = \begin{bmatrix}5&-2\\-1&6\\\end{bmatrix}$$
Разделим все элементы матрицы $$adj A^T$$ на определитель исходной матрицы $$A$$
$$A^{-1}=\begin{bmatrix}\frac{5}{28}&\frac{-2}{28}\\\frac{-1}{28}&\frac{6}{28}\\\end{bmatrix}=\begin{bmatrix}\frac{5}{28}&-\frac{1}{14}\\-\frac{1}{28}&\frac{3}{14}\\\end{bmatrix}=\begin{bmatrix}0.178571428571429&-0.0714285714285714\\-0.0357142857142857&0.214285714285714\\\end{bmatrix}$$