Калькулятор умножения матриц
Данный калькулятор дает детальное решение с объяснением умножения двух матриц.
Умножить две матрицы возможно только в том случае, если количество столбцов первой матрицы, равно количеству строк второй.
| Десятичные дроби
|
Ввод
|
| $$3,9$$
|
3.9
|
| $$6,012$$
|
6.012
|
| $$0,209$$
|
0.209
|
| Обыкновенные дроби
|
|
| $$\dfrac{2}{3}$$
|
2/3
|
| $$\dfrac{15}{7}$$
|
15/7
|
| $$\dfrac{1}{9}$$
|
1/9
|
| Возведение в степень
|
|
| $${3}^{2}$$
|
3^2
|
| $${{2}^{3}}^{4}$$
|
(2^3)^4
|
| $$\left({\dfrac{2}{3}}\right)^{8}$$
|
(2/3)^8
|
| Квадратный корень
|
|
| $$\sqrt{2}$$
|
sqrt(2)
|
| $$\sqrt{\dfrac{9}{15}}$$
|
sqrt(9/15)
|
| $$\left(\sqrt{\dfrac{6}{7}}\right)^{3}$$
|
(sqrt(6/7))^3
|
| $$2\sqrt{5}$$
|
2*sqrt(5)
|
| $$\dfrac{1}{2}\sqrt{3}$$
|
(1/2)*sqrt(3)
|
| Число π
|
|
| $$\pi$$
|
pi
|
| $$2\pi$$
|
2pi
|
| $$\dfrac{3\pi}{2}$$
|
3pi/2
|
| Число Эйлера e
|
|
| $$e$$
|
Для записи числа Эйлера введите e
|
| $${e}^{\left(\dfrac{1}{3}\right)}$$
|
e^(1/3)
|
| Натуральный логарифм ln
|
|
| $$\ln{3}$$
|
ln(3)
|
| $$\ln{\dfrac{1}{2}}$$
|
ln(1/2)
|
| $$\sqrt{\ln{5}}$$
|
sqrt(ln(5))
|
| Экспоненциальная запись чисел
|
|
| $$2.3e+15$$
|
2.3e+15
|
| $$2.45e-35$$
|
2.45e-35
|
| Абсолютная величина (модуль) |
|
| $$\lvert -5 \rvert$$
|
abs(-5)
|
| $$\lvert \sqrt{2}-7 \rvert$$
|
abs(sqrt(2)-7)
|
| Тригонометрические функции
|
|
| Внимание! Параметр x должен быть указан в радианах. Если вам необходимо выполнить вычисления в градусах, то необходимо внутри функции сделать перевод из градусов в радианы, например, sin(45°), тогда sin(45*pi/180).
|
|
| Синус sin(x) |
sin(x) |
| Косинус cos(x) |
cos(x) |
| Тангенс tg(x), tan(x) |
tan(x) |
| Котангенс ctg(x), cot(x) |
cot(x) |
| Секанс sec(x) |
sec(x) |
| Косеканс csc(x), cosec(x) |
csc(x) |
| Гиперболические функции
|
|
| Внимание! Параметр x должен быть указан в радианах. Если вам необходимо выполнить вычисления в градусах, то необходимо внутри функции сделать перевод из градусов в радианы, например, sinh(45°), тогда sinh(45*pi/180).
|
|
| Гиперболический синус sh(x), sinh(x) |
sinh(x) |
| Гиперболический косинус ch(x), cosh(x) |
cosh(x) |
| Гиперболический тангенс th(x), tanh(x) |
tanh(x) |
| Гиперболический котангенс cth(x), coth(x) |
coth(x) |
| Гиперболический секанс sch(x), sech(x) |
sech(x) |
| Гиперболический косеканс csch(x), csch(x) |
csch(x) |
| Обратные тригонометрические функции
|
|
| Арксинус arcsin(x) |
asin(x) |
| Арккосинус arccos(x) |
acos(x) |
| Арктангенс arctg(x), arctan(x) |
atan(x) |
| Арккотангенс arcctg(x), arccot(x) |
acot(x) |
| Арксеканс arcsec(x) |
asec(x) |
| Арккосеканс arccsc(x) |
acsc(x) |
| Обратные гиперболические функции
|
|
| Ареасинус arsh(x), arsinh(x), sin−1 |
asinh(x) |
| Ареакосинус arch(x), arcosh(x), cosh−1 |
acosh(x) |
| Ареатангенс arth(x), artanh(x), tanh−1 |
atanh(x) |
| Ареакотангенс arcth(x), arcoth(x), coth−1 |
acoth(x) |
| Ареасеканс arsch(x), arsech(x), sech−1 |
asech(x) |
| Ареакосеканс arcsch(x), csch−1 |
acsch(x) |
| Математические выражения
|
|
| $$\dfrac{3}{\sqrt{2}} + \left({\dfrac{3}{2}}\right)^{5}$$
|
3/sqrt(2)+(3/2)^5
|
| $$\dfrac{3}{\sqrt{2}\cdot\dfrac{1}{12}-\dfrac{4}{3}}$$
|
3/(sqrt(2)*(1/12)-3/4)
|
| $${\left(\dfrac{5}{12} + \dfrac{3}{2} - 5\right)}^{\dfrac{1}{2}}$$
|
(5/12 + 3/2 - 5)^(1/2)
|
| $$6-7\cos{\frac{3\pi}{2}}^{2}$$
|
6-7*cos(3*pi/2)^2
|
Как умножать матрицы
Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.
Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Две матрицы A и B можно умножить только в том случае, если число столбцов матрицы A равно числу строк матрицы B.
При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n
$$C = A \cdot B=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\\a_{41}&a_{42}\\\end{bmatrix} \cdot \begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\\end{bmatrix} = \begin{bmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\c_{41}&c_{42}&c_{43}\\\end{bmatrix} $$
Как видно если размерность матрица A 4 × 2, матрицы B 2 × 3, то размерность исходной матрицы C будет 4 × 3.
Элемент матрицы C с индексом cij находится по формуле
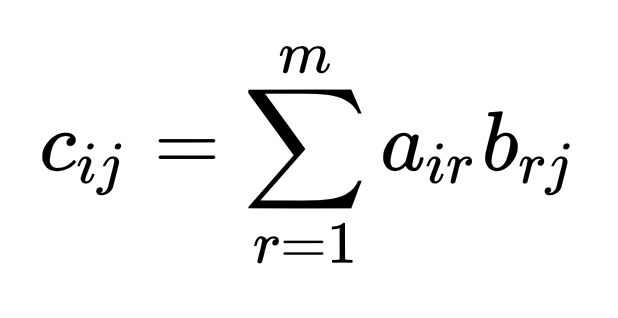
Приведем пример, умножим две матрицы A и B. Размер матрицы A равен 3 ×
2, размер матрицы B равен 2 × 3.
$$A \cdot B=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\\\end{bmatrix} \cdot \begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\\end{bmatrix} = \begin{bmatrix} \left(a_{11} \cdot b_{11}\right)+ \left(a_{12} \cdot b_{21}\right)& \left(a_{11} \cdot b_{12}\right)+ \left(a_{12} \cdot b_{22}\right)& \left(a_{11} \cdot b_{13}\right)+ \left(a_{12} \cdot b_{23}\right)\\ \left(a_{21} \cdot b_{11}\right)+ \left(a_{22} \cdot b_{21}\right)& \left(a_{21} \cdot b_{12}\right)+ \left(a_{22} \cdot b_{22}\right)& \left(a_{21} \cdot b_{13}\right)+ \left(a_{22} \cdot b_{23}\right)\\ \left(a_{31} \cdot b_{11}\right)+ \left(a_{32} \cdot b_{21}\right)& \left(a_{31} \cdot b_{12}\right)+ \left(a_{32} \cdot b_{22}\right)& \left(a_{31} \cdot b_{13}\right)+ \left(a_{32} \cdot b_{23}\right)\\\end{bmatrix} $$
$$A \cdot B=\begin{bmatrix}3&-1\\7&9\\0&-5\\\end{bmatrix} \cdot \begin{bmatrix}4&2&1\\3&-9&11\\\end{bmatrix} = \begin{bmatrix}\left(3 \cdot 4\right)+\left(-1 \cdot 3\right)&\left(3 \cdot 2\right)+\left(-1 \cdot \left(-9\right)\right)&\left(3 \cdot 1\right)+\left(-1 \cdot 11\right)\\\left(7 \cdot 4\right)+\left(9 \cdot 3\right)&\left(7 \cdot 2\right)+\left(9 \cdot \left(-9\right)\right)&\left(7 \cdot 1\right)+\left(9 \cdot 11\right)\\\left(0 \cdot 4\right)+\left(-5 \cdot 3\right)&\left(0 \cdot 2\right)+\left(-5 \cdot \left(-9\right)\right)&\left(0 \cdot 1\right)+\left(-5 \cdot 11\right)\\\end{bmatrix} = \begin{bmatrix}9&15&-8\\55&-67&106\\-15&45&-55\\\end{bmatrix}$$
$$ A \cdot B=\begin{bmatrix}9&15&-8\\55&-67&106\\-15&45&-55\\\end{bmatrix}$$