Векторное произведение векторов
Векторным произведением двух векторов $$\overline{a}$$ и $$\overline{b}$$ в трехмерном евклидовом пространстве – называется вектор $$\overline{c}$$. Модуль вектора $$\overline{c}$$, численно равен площади параллелограмма $$OABQ$$, построенного на векторах $$\overline{a}$$ и $$\overline{b}$$, то есть $$|\overline{c}|$$ = $$|\overline{a}||\overline{b}|\sin{\angle\overline{a}\overline{b}}$$.
Векторное произведение векторов $$\overline{a}$$ и $$\overline{b}$$ обозначается как: $$[\overline{a}\overline{b}]$$, $$[\overline{a},\overline{b}]$$, $$\overline{a}\times\overline{b}$$, $$\overline{a}\wedge\overline{b}$$
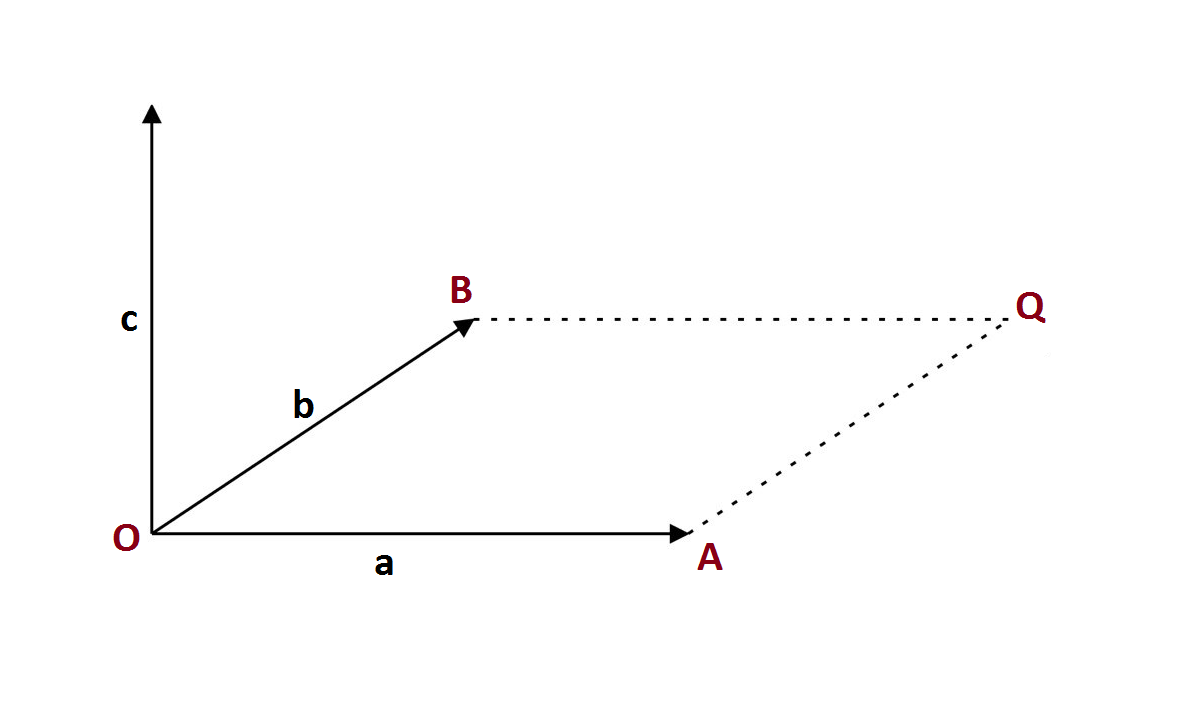Параллелограмм $$OABQ$$
Направление получившегося вектора $$\overline{c}$$ будет перпендикулярно плоскости параллелограмма $$OABQ$$.
В правом ортонормированном базисе векторное произведение векторов определяется как:
$$\overline{a} \times \overline{b} = \{ a_y b_z - a_z b_y \, ; \, a_z b_x - a_x b_z \, ; \, a_x b_y - a_y b_x\}$$
Формула для координат векторного произведения вычисляется из определителя третьего порядка, где первая строка – векторы $$i$$, $$j$$, $$k$$
$$\overline{i} = \left\{1\, ; \,0\, ; \,0\right\}$$,
$$\overline{j} = \left\{0\, ; \,1\, ; \,0\right\}$$,
$$\overline{k} = \left\{0\, ; \,0\, ; \,1\right\}$$,
а вторая и третья строки – координаты векторов $$\overline{a}$$ и $$\overline{b}$$:
$$\overline{a} \times \overline{b} = \begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\a_x&a_y&a_z\\b_x&b_y&b_z\\\end{vmatrix} = \overline{i}\begin{vmatrix}a_{y}&a_{z}\\b_{y}&b_{z}\\\end{vmatrix}-\overline{j}\begin{vmatrix}a_{x}&a_{z}\\b_{x}&b_{z}\\\end{vmatrix}+\overline{k}\begin{vmatrix}a_{x}&a_{y}\\b_{x}&b_{y}\\\end{vmatrix}=$$
$$ \overline{i}\,a_yb_z - \overline{i}\, a_zb_y - \overline{j}\, a_xb_z + \overline{j}\, a_zb_x +\overline{k}\, a_xb_y - \overline{k}\, a_yb_x =$$
$$\overline{i}(a_yb_z - b_ya_z) - \overline{j}(a_xb_z - b_xa_z) + \overline{k}(a_xb_y - b_xa_y)$$
Векторное произведение не обладает переместительным свойством, поэтому при перестановке множителей векторное произведение изменит знак:
$$\overline{b} \times \overline{a} = -(\overline{a} \times \overline{b})$$
Векторное произведение равно нулю, когда векторы $$\overline{a}$$ и $$\overline{b}$$ коллинеарны (параллельны, т.е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.
В левом ортонормированном базисе векторное произведение векторов определяется как:
$$ \overline{a} \times \overline{b} = \{ a_z b_y - a_y b_z \, ; \, a_x b_z - a_z b_x \, ; \, a_y b_x - a_x b_y\}$$
Примеры векторного произведения векторов
Пример 1. Найдем векторное произведение векторов в правом ортонормированном базисе. Координаты обоих векторов заданны точками.
Координаты точки $$A$$ равны: $$A(2\,;\,4\,;\,-5)$$.
Координаты точки $$B$$ равны: $$B(3\,;\,-9\,;\,7)$$.
Координаты точки $$C$$ равны: $$C(-1\,;\,5\,;\,-2)$$.
Координаты точки $$D$$ равны: $$D(9\,;\,4\,;\,12)$$.
Вычислим координаты первого вектора по двум точкам $$A$$ и $$B$$
$$\overline{AB} = \{B_x - A_x \,;\, B_y - A_y \,;\, B_z - A_z\}$$
$$\overline{AB} = \left\{3 - 2\, ; \,-9 - 4\, ; \,7 - \left(-5\right)\right\} = $$$$\left\{1\, ; \,-13\, ; \,12\right\}$$
Вычислим координаты второго вектора по двум точкам $$C$$ и $$D$$
$$\overline{CD} = \{D_x - C_x \,;\, D_y - C_y \,;\, D_z - C_z\}$$
$$\overline{CD} = \left\{9 - \left(-1\right)\, ; \,4 - 5\, ; \,12 - \left(-2\right)\right\} = $$$$\left\{10\, ; \,-1\, ; \,14\right\}$$
$$\overline{AB} = \left\{1\, ; \,-13\, ; \,12\right\}$$
$$\overline{CD} = \left\{10\, ; \,-1\, ; \,14\right\}$$
В правом ортонормированном базисе векторное произведение векторов $$\overline{AB}$$ и $$\overline{CD}$$ вычисляется по формуле:$$\overline{AB} \times \overline{CD} = \{ AB_y CD_z - AB_z CD_y \, ; \, AB_z CD_x - AB_x CD_z \, ; \, AB_x CD_y - AB_y CD_x\}$$
$$\overline{AB} \times \overline{CD} = $$$$\left\{\left(-13 \cdot 14 \right) - \left(12 \cdot \left(-1\right) \right)\, ; \,\left(12 \cdot 10 \right) - \left(1 \cdot 14 \right)\, ; \, \left(1 \cdot \left(-1\right) \right) - \left(-13 \cdot 10 \right)\right\} = $$$$\left\{-170\, ; \,106\, ; \,129\right\}$$
$$\overline{AB} \times \overline{CD} = $$$$\left\{-170\, ; \,106\, ; \,129\right\}$$
Пример 2. Найдем векторное произведение векторов в правом ортонормированном базисе.
$$\overline{a} = \left\{5\, ; \,1\, ; \,7\right\}$$
$$\overline{b} = \left\{2\, ; \,4\, ; \,6\right\}$$
В правом ортонормированном базисе векторное произведение векторов $$\overline{a}$$ и $$\overline{b}$$ вычисляется по формуле:
$$\overline{a} \times \overline{b} = \{ a_y b_z - a_z b_y \, ; \, a_z b_x - a_x b_z \, ; \, a_x b_y - a_y b_x\}$$
$$\overline{a} \times \overline{b} = $$$$\left\{\left(1 \cdot 6 \right) - \left(7 \cdot 4 \right)\, ; \,\left(7 \cdot 2 \right) - \left(5 \cdot 6 \right)\, ; \, \left(5 \cdot 4 \right) - \left(1 \cdot 2 \right)\right\} = $$$$\left\{-22\, ; \,-16\, ; \,18\right\}$$
$$\overline{a} \times \overline{b} = $$$$\left\{-22\, ; \,-16\, ; \,18\right\}$$